A Pattern of Numbers

 

fullnum

I’m not entirely sure what this is. Only that it has been stuck in my head for close to 15 years now.
I am aware of some of the more contemporary history of the Arabic (Hindu) numerals that we use and that these are derived from.
From that I know that the patterns that I am exploring in these shapes were probably not intentionally put there- many hands and minds touched these shapes on their way to our modern usage of them.

The pattern in the higher primes and their multiples is probably known and I have probably gone through a strange and roundabout way to find a generally useless but curious anomaly. But, I just needed to get this out there and see what people think- drop me a line and let me know.

This will probably grow. 

 

 147

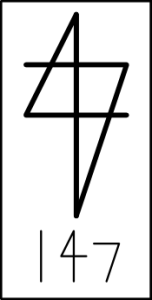
The 1 and the 7 are the stick and the angle respectively. The 4 combines the stick and the angle- the 1 and 7 are prime, the 4 is not.

  258

The 2 hooks the top, crossing the bottom and the 5 hooks the bottom, crossing the top. The 8 encircles both- the 2 and 5 are prime, the 8 is not.

  369

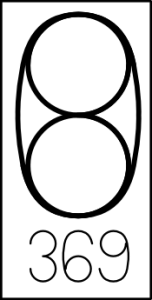
The 6 circles the bottom and hooks the top and the 9 circles the top and hooks the bottom. The 3 hooks the top and bottom- 3 is prime, while 6 and 9 are not.
1 2 3
4 5 6
7 8 9
10-1 11-2 12-3
13-4 14-5 15-6
16-7 17-8 18-9
19-1 20-2 21-3
22-4 23-5 24-6
25-7 26-8 27-9
  In numerology, the “root” of a number is found by adding all of it’s digits, if this results in a number with more than one digit, these are then added until you get a single digit- this is the numerological root.
Here you can see the 1-4-7, 2-5-8 and 3-6-9 sequence continues on infinitely, it makes sense, there’s no reason for it not to. 

 
1 2 3
4 5 6
7 8 9
1 2 3
4 5 6
7 8 9
1 2 3
4 5 6
7 8 9
1 2 3
4 5 6
7 8 9
1 2 3
4 5 6
7 8 9
1 2 3
4 5 6
7 8 9
1 2 3
4 5 6
7 8 9
When we start looking at the patterns of multiplication, it gets kind of interesting- the 2 times table is a nice checker board.

The 3 times table is the whole last column and, of course, it also contains the 6s and 9s- the 6s are all the even ones and the 9s are the ones whose “root” is 9.

Red – multiple of 6 (even)

Yellow – multiple of 9 (root 9)

Orange – multiple of 6 and 9 (even, root 9)

 

 
5
1
6
2
7
3
8
4
9
 Here we have the 5 times table. Note that as it bounces through each column, it hits on each root cyclically,albeit in a different order: 1-7-4, 5-2-8 and 6-3-9.

The 5 times table is fun because you can do it in your head- the “root 9” at the end of the table is from 45- from there it goes 5 (50), 1 (55), 6 (60), 2 (65), 7 (70), 3 (75), 8 (80), 4 (85) and back to 9 (90).

If you look back to the 2s, you will see that it does the same thing (just with a different starting point); 4-1-7, 2-8-5 and 6-3-9.

Higher Primes and Their Multiples

 

+6 +4 +2 +4 +2 +4 +6 +2
7 11 13 17 19 23 29 31
37 41 43 47 49 53 59 61
67 71 73 77 79 83 89 91
97 101 103 107 109 113 119 121
127 131 133 137 139 143 149 151
157 161 163 167 169 173 179 181

 

This is when I dug a little deeper (or perhaps went off the rails), when I coloured all the multiples of the lower numbers and found a pattern in the “holes”. In the table, the + numbers at the top of each column is what was added to the previous number to get the number shown.

So, starting from 1 (not shown), we +6 to get 7, +4 to get 11, +2 to get 13 and so on.
The pattern of numbers that emerges is quite interesting.
 Looking at each of the columns, I noticed 2 striking things:

1. all the numbers in a given column end in the same digit
2. each column has a 1-4-7 or 2-5-8 root pattern

The other thing to note about this overall set is that it contains only primes and multiples of other numbers in the set.
To demonstrate:
7×7 = 49
7×11 = 77
7×13 = 91
7×17 = 119
7×19 = 133
7×23 = 161
11×11 = 121
11×13 = 143
13×13 = 169

After eliminating 49, 77, 91, 119, 133, 161, 121, 143, 169 from the above table, all the remaining numbers are prime.
This opens a few possibilities for exploring primes- generate the set, calculate the multiples and remove them from the set, leaving only primes, or use the combination of the final digit and numerological root to find higher numbers that are part of the sequence and then test for factors using numbers from the set to see if it’s a prime (possibly saving a large amount of redundant checks).

Or maybe not, but this is the idea that’s been buzzing around my brain and needed to get out, hope it stirs some brain cells.

An entry point to the world of WEBmadman